Geometri – Uge 4 – Januar – Dag 1 og 2

Hej alle sammen.

Hermed programmet for uge 4. Vi arbejder hovedsageligt med kapitel 2 i denne uge.

Dag 1

Grupper til praktik på Hunderupskolen?!
Evaluering af modul 1.
Ugens program
1. Geogebratube og Geogebrabooks.
2. Opgaver fra grundbogen Kapitel 2: Øvelserne 12-16 samt undersøgelse 3.
3. Besøge CFU og finde opgaver.
  1. Finde færdigheds- og vidensmål. som omhandler stoffet i kapitel 2.
  2. Udvælg 2-3 opgaver, som du mener, kan bruges i forhold til de områder, som du har lært om i kapitel 2.
  3. Løs selv opgaverne i Geogebra og gør dig klar til at præsentere opgaverne.
Modulprøve – feedback og dato for reeksamen.

Dag 2

Praktikken: Hvem er tovholder i grupperne på praktikskolerne?
Modulevaluering via Fronter (Først individuel + Fælles afsluttende evaluering og snak om rapporten)
Undervejs i dag vil jeg gennemgå modulprøven med jer alle.
Individuel øvelse:
1. Besøge CFU.
2. Find (evt. flere, hvis du blev “færdig” sidste gang) opgaver til opgaven (fra sidste gang), som passer til kapitel 2.
3. Hvordan ville du kort overfor dine medstuderende
  1. præsentere området? (Altså, hvad handler kapitlet om? Hvad skal man lære?)
  2. præsentere målene for en eller flere af opgaverne? (FFM + Læringsmål, se på emu)
  3. præsentere opgaverne, som du har udvalgt?
  4. gøre opgaverne til en gruppeøvelse?
  5. lave en “aktiv” øvelse? (genstandsmæssig/kropslig præsentation),
  6. lave opgaven i Geogebra og
  7. lave en eller flere af opgaverne til eksperimenterende øvelser i Geogebra.
Gruppeøvelse:
1. Én efter én skal I nu for de andre medstuderende i grupperne
  1. overordnet præsentere området,
  2. præsentere målene (FFM + læringsmål, husk også matematiske kompetencer) for en eller flere af opgaverne,
  3. præsentere de opgaver, som I har udvalgt,
  4. lave en eller flere af opgaverne som en gruppeøvelse,
  5. lave en aktiv øvelse,
  6. lave opgaverne i Geogebra,
  7. drøfte og afprøve, hvorvidt man kan lave en eller flere af opgaverne til eksperimenterende øvelser i Geogebra.
2. Afprøv opgaverne og snak om, hvor I tror, at elever vil
  1. blive udfordrede?
  2. blive motiverede?
Arbejde med de resterende opgaver i bogens kapitel 2.

Hjælp

Øvelse 12

Skriv (2,3)

Skriv v=Vektor[ (4,4) ]

Skriv Parallelforskyd[ v, A ]

Skriv Parallelforskyd[ v + v +v, A ]

Skriv Parallelforskyd[6*v, A]

Se evt. løsning ggbm.at/UFtJDrpa.

Øvelse 13

ggbm.at/X4hhAPKJ

Hint! Kig på x og y-koordinaterne for hver vektor.

Undersøgelse 3

Afprøv med funktionerne i inputfeltet:

A = (2,2)

Vektor[ <Punkt> ] (skriv fx Vektor[ (6,4)]

Parallelforskyd[ <Vektor>, <Start punkt> ] (skriv fx Parallelforskyd[6*u, A] eller Parallelforskyd[u+u, A]

Punkt[ <Punkt>, <Vektor> ] (Denne funktion afsætter et punkt for enden af vektoren)

Opgave 1

Opgave 2 (se ggbm.at/U3aGFtEN)

C. Skriv evt. i inputfeltet F=(x(B)*3,y(B)*3) og Parallelforskyd[f*3, O]

Den retlinjede bevægelse

Øvelse 14

Kig på figur 1 på side 37 (se den her ggbm.at/H4RgjZqk)

Punkt A = (-5,-2)

Vektoren = (3,4)

Efter 20 minutter er han nået $\frac{1}{3}$ ud af vektoren (3,4), dvs. nået ud til begyndelsespunktet plus $\frac{1}{3}$ af vektoren (3,4): $\left(\frac{1}{3}\cdot 3, \frac{1}{3}\cdot 4 \right) = \left(1, \frac{4}{3} \right)$ , altså til (-5,-2) + $\left(1, \frac{4}{3} \right) = \left(-4, -\frac{2}{3} \right)$ .

Efter en halv time er han kommet til begyndelsespunktet plus det halve af vektoren (3,4):

$\left(\frac{1}{2}\cdot 3, \frac{1}{2}\cdot 4 \right) = \left(\frac{3}{2},2 \right)$ , altså til (-5,-2) + $\left(\frac{3}{2},2 \right) = \left(- \frac{7}{2},0 \right)$ .

Efter to timer er han kommet dobbelt så langt, altså begyndelsespunktet plus 2 gange vektoren (3,4): (2⋅3,2⋅4)=(6,8), altså til (-5,-2) + (6,8) = (1,6).

Generelt kan vi se, at til tiden t er han nået til begyndelsespunktet plus vektoren (3t, 4t), således at svar nr. 2 er det korrekte.

I Geogebra kan man afsætte vektoren først med Vektor [ (3,4) ] og derefter fx bruge Parallelforskyd[u*0.5 , A].

Jeg har også tegnet det i Geogebra her ggbm.at/G8WJqZKC.

I kan også bruge funktionen Kurve[-5+3*t, -2+4*t, t, 0, 3]

Øvelse 15

En behagelighed ved denne tur er at Ali kommer hjem igen, idet

P(0) = (-5 + 0, -2 – 0) = (-5,-2)

P(3) = (4 – 9, 10 – 12) = (-5,-2)

Altså er

P(0) = (-5 + 0, -2 – 0) = (4 – 9, 10 – 12) = P(3).

I kan tegne positionsfunktionerne P(t) vha. kurve-funktionen i Geogebra. Skriv :

Kurve[-5+4*t, -2-t, t, 0,1]
Kurve[-t, -8+5*t, t, 1,2]
Kurve[4-3*t, 10-4*t, t, 2,3]

Se løsningen her ggbm.at/fzf8XuND.

Skal man afgøre, om han på noget tidspunkt går hurtigere end 5 km i timen, skal man se på koefficienterne til t på de to koordinater. I intervallet [1,2[ ser vi, at der står hhv. –t og 5t, hvilket betyder, at han på en time bevæger sig 1 km (tilbage) i x-aksens retning og 5 km opad i y-aksens retning, hvilket klart sammenlagt giver mere end 5 km – dog ikke 6, idet han jo bevæger sig direkte og ruten beregnes ved Pythagoras’ sætning til $\sqrt{5^2 + 1^2} = \sqrt{26} >5 km/t$ .

Øvelse 16

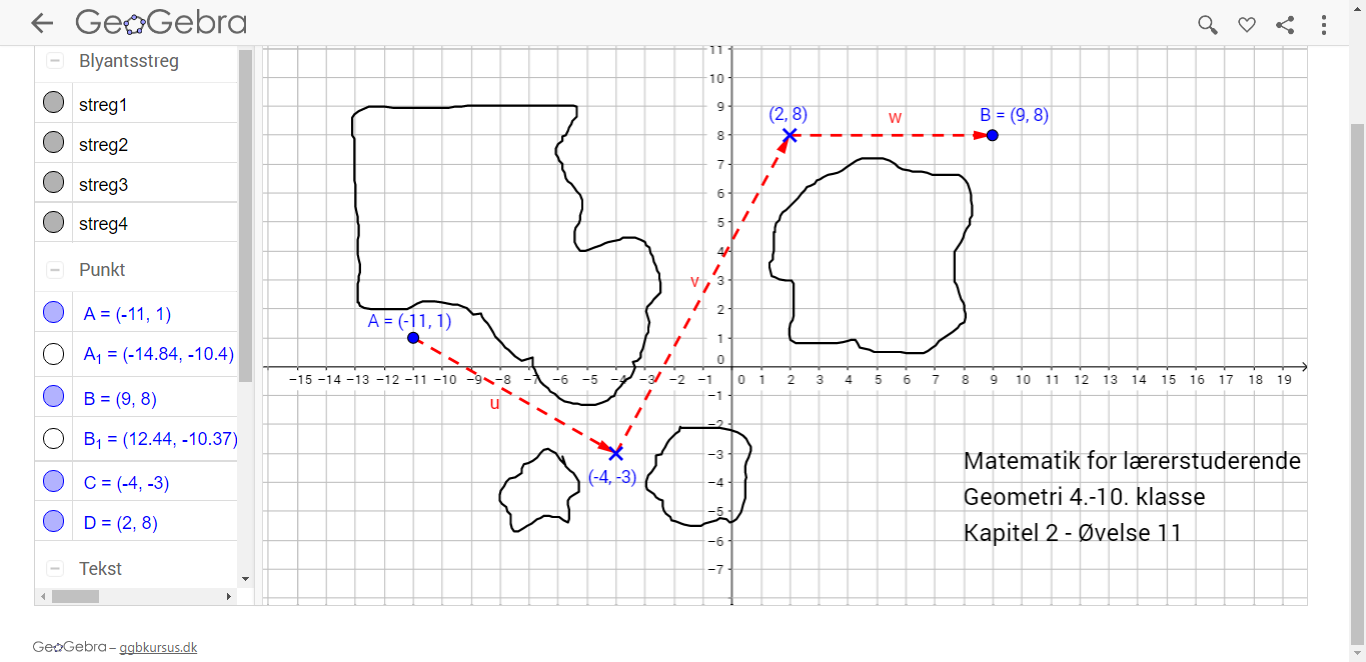
I denne opgave er der flere løsningsmuligheder, da I i øvelse 11 selv kan indtegne jeres egne vektorer fra A til B.

Se en mulig løsning af øvelse 11 her: ggbm.at/GVfAYA4x.

I mit tilfælde er løsningen fx.

A=(-11,1)

P(t) = (-11 + 7 * t, 1 – 4 * t) for t i intervallet [0,1[ se fx kurve[-11 + 7*t, 1 – 4*t,t,0,1].

P(t) = (-10 + 6 * t, -14 + 11 * t) for t i intervallet [1,2[ se fx Kurve[-10 + 6*t, -14 + 11*t, t, 1, 2]

P(t) = (-12 + 7 * t, 8) for t i intervallet [2,3] se fx Kurve[-12 + 7*t, 8 , t, 2, 3]

Se linket her: ggbm.at/HMDztzcY

Matematik

Matematik for lærerstuderende