Hermed programmet for uge 4. Vi arbejder hovedsageligt med kapitel 3 om “Undersøgelse af rumlige figurer” i denne uge.

DAG 1

Program

1. Praktik – grupper og kompetenceprøven – nye grupper
2. Afsluttende feedback og feedforward på modulprøven samt afslutning af opgaven fra sidste gang.
   1. Gå i gang med at læse kapitel 3.
3. Lokale B208 kl. 12.30 i morgen vedrørende praktikken.
4. Arbejde med kapitel 3 og papir.

Dag 2

Program

1. Opsamling vedr. praktik – grupper, opgaven og eksamen
2. Kapitel 4
3. Videoøvelse
4. Fortsættelse af opgaverne i bogen.
5. Afsluttende arbejde med praktikken.

Hjælp til kapitel 3

Rumlige figurer – Genopdagelse af platoniske legemer

Ved et polyeder forstår man overfladen på et rumligt legeme, der er afgrænset af et endeligt antal plane polygoner. Disse polygoner kaldes polyederets sideflader. De linjestykker, der begrænser sidefladerne, kaldes polyederets kanter, og kanternes endepunkter kaldes polyederets hjørnespidser.

Eller sagt på en anden måde:

• Et polygon er oversat en mangekant eller en flerkant.
• Et polyeder består således af flere polygoner.
• Ved et regulært polyeder er sidefladerne kongruente regulære polygoner og alle hjørner er ens.

Øvelse 1

1)

I regulære polygoner er alle sider lige lange og alle vinkler er lige store.

2)

Afprøv evt. ved at lave Tetraede.

3)

I kan tage udgangspunkt i disse, men også lave jeres egne. Ikke alle herunder er nødvendivis regulære polyeder.

5-sidet pyramide 6 sidet terning 12 sidet terning – med tal 12 sidet terning – uden tal Kasse-Højhus Oktaede Tetraede 4-sidet pyramide

Prøv i Geogebra at vise 3D Grafik.

• Tetraeder[ <Punkt>, <Punkt> ]  (Prøv fx at skrive “Tetraeder[(0,0), (3,0) ]” i inputfeltet.)
• Kube[ <Punkt>, <Punkt> ]   (Det er hexaeden)
• Oktaeder[ <Punkt>, <Punkt> ]
• Dodekaeder[ <Punkt>, <Punkt> ]
• Ikosaeder[ <Punkt>, <Punkt> ]

Se evt. filmen nedenfor.

4)

Undersøg først. I kan fx anvende Geogebra. Markér teksten i parentesen ( Ja, han har ret ).

5)

Tetraede (4) 6 sidet terning(6 – hexaede) Oktaede (8) 12 sidet terning – uden tal (12 dodakaede)

Eulers polyedersætning

Undersøgelse 1

Undersøgelse 2

• Geometric Solids – illuminations.nctm.org/activity.aspx?id=3521
• Cut-outs, Nets – www.fi.uu.nl/toepassingen/00297/toepassing_wisweb.en.html (JAVA – Kør i Firefox)
• A Plethora of Polyhedra – virker ikke mere – http://www.uff.br/cdme/pdp/pdp-html/pdp-en.html
• Geogebra – Prøv at konstruere dem og lav “Udfoldning” i 3D grafik.

Descartes’ spidsheder

Undersøgelse 3

Vær opmærksom på, at defekten = 360 – vinkelsummen.

De skelner mellem defekten i toppen/spidsen af pyramiden og defekten i hjørnerne af pyramiden. Når spidsen af pyramiden bliver meget spids, så er vinkelsummen i spidsen meget lille (næsten 0). Dermed bliver defekten = 360 – 0 = 360. I hjørnerne er der 3 vinkler, som nærmer sig 90 grader. Dvs. vinkelsummen bliver 3 * 90 = 270. Defekten i hjørnerne bliver derfor = 360 – 270 = 90, når vinkelspidsen i pyramiden bliver meget spids (og dens defekt bliver = 360 ).

Undersøgelse 4

Se evt.

https://no.wikipedia.org/wiki/Arkimedisk_legeme

Navn	Gjennomsiktig	Figur	Flat	Overflater		Kanter	Hjørner
Avstumpet tetraeder (3,6,6)	(animasjon)			8	4 trekanter 4 heksagoner	18	12
Kuboktaeder (3,4,3,4)	(animasjon)			14	8 trekanter 6 kvadrater	24	12
Avstumpet kube (3,8,8)	(animasjon)			14	8 trekanter 6 oktogoner	36	24
Avstumpet oktaeder (4,6,6)	(animasjon)			14	6 kvadrater 8 heksagoner	36	24
Rombkuboktaeder (3,4,4,4)	(animasjon)			26	8 trekanter 18 kvadrater	48	24
Avstumpet kuboktaeder (4,6,8)	(animasjon)			26	12 kvadrater 8 heksagoner 6 oktogoner	72	48
Sløv kube (3,3,3,3,4)	(animasjon)			38	32 trekanter 6 kvadrater	60	24
Ikosidodekaeder (3,5,3,5)	(animasjon)			32	20 trekanter 12 pentagoner	60	30
Avstumpet dodekaeder (3,10,10)	(animasjon)			32	20 trekanter 12 dekagoner	90	60
Avstumpet ikosaeder (5,6,6)	(animasjon)			32	12 pentagoner 20 heksagoner	90	60
Rombikosidodekaeder (3,4,5,4)	(animasjon)			62	20 trekanter 30 kvadrater 12 pentagoner	120	60
Avstumpet ikosidodekaeder (4,6,10)	(animasjon)			62	30 kvadrater 20 heksagoner 12 dekagoner	180	120
Sløvt dodekaeder (3,3,3,3,5)	(animasjon)			92	80 trekanter 12 pentagoner	150	60

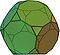
Til slutt kan pseudorombkuboktaederet per defenisjon både reknes og ikke reknes som et arkimedisk legeme:

Navn	Gjennomsiktig	Figur	Flat	Overflater		Kanter	Hjørner
Pseudorombkuboktaeder				26	8 trekanter 18 kvadrater	48	24

Undersøgelse 5

tavlebog.dk

Hjælp til kapitel 4

Øvelse 1

Øvelse 2

1)

Vi antager, at l er parallel med m, og m er parallel med n. Vi skal vise, at l er parallel med n. Det gør vi med et indirekte bevis.
Vi antager, at l skærer n i et punkt P. Gennem punktet P har vi nu ifølge det forudsatte to linjer, der er parallelle med m, men ifølge aksiom 3 kan der igennem punktet P kun trækkes en linje parallel med m. Altså er l lig med n. Vi har hermed vist, at enten er l parallel med n eller også er l lig med n, og så er de også parallelle (definition 3).

2)

Det er ikke noget bevis inden for den Euklidiske ramme, fordi det ikke bygger på definitioner, aksiomer og sætninger, vi allerede har vist, men derimod bygger på noget, vi af anden vej ved om parallelle linjer.

Øvelse 3

Formlen kan findes ved at dele n-kanten op i (n−2) trekanter. Man får vinkelsummen (n−2)⋅180°.

Øvelse 4

1)

∠C og nabovinklen z udgør tilsammen to rette. Vi ved også, at ∠A+∠B+∠C også er to rette. Vi har altså i kort notation: z + C = A + B + C. Ifølge den 3. almene lov må vi gerne trække det samme fra på hver side, og vi ender med z = A + B, hvilket skulle bevises.

2)

Det er ikke nok oplysninger til at bestemme alle tre vinkler.

3)

Oplysningerne giver tre ligninger: B + C = 100; A + C = 150 og A + B = 90. Løses disse ligninger fås A = 70, B = 20 og C = 80. Men det kan ikke lade sig gøre. Den samlede vinkelsum bliver kun 170. Trekanten eksisterer altså ikke.