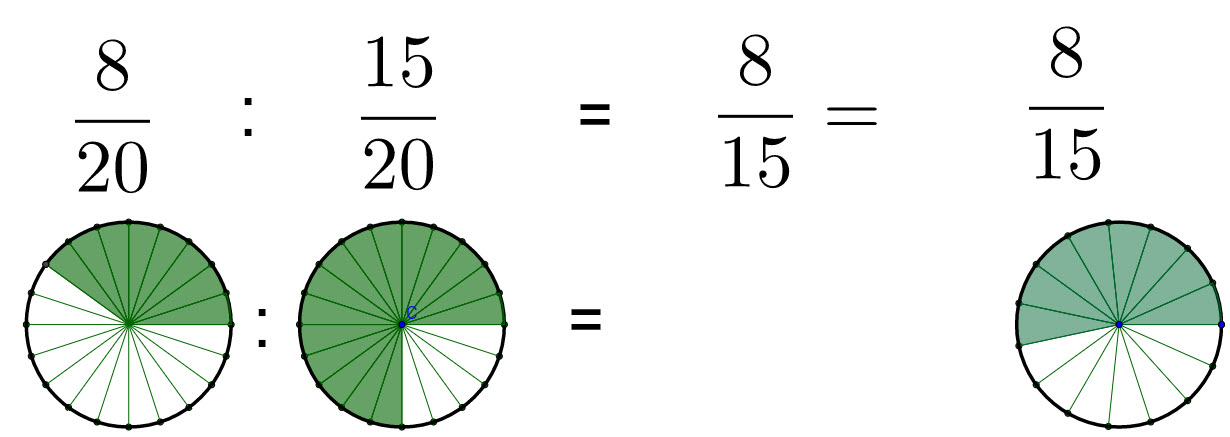M1-1E17NET – Program – 2017 – Uge 41– Dag 2

Kapitel 5 – De positive rationale tal

Brøker

Bogens fortolkning af brøker kan kort formuleres således:

En brøk er en ligelig opdeling af en enhed. Vi deler en enhed i b lige store dele. Fx kan vi dele 20 æg i 4 lige store dele, hvilket er 5 æg til hver fjerdedel.
Hver af disse dele kalder vi en b’endedel, hvilket skrives som $\frac{1}{b}$ .
a bliver da en angivelse af, hvor mange af de $\frac{1}{b}$ .’endedele, vi tager. Vi tager $a \cdot \frac{1}{b}$ , hvilket skrives som $\frac{a}{b}$ . Fx tager vi 3 af $\frac{1}{4}$ , hvor hver fjerdedel svarer til 5 æg. Det giver samlet 15 æg. Så $\frac{3}{4}$ af 20 æg er lig med 15 æg.

Sætning 1 – At forkorte og forlænge brøker

Brøker kan multipliceres med samme hele tal i tæller og nævner, uden at brøken derved ændrer størrelse. Dette kan udtrykkes symbolsk som:

Forlængning: $\frac{a}{b} = \frac{n\cdot a}{n \cdot b}$ Forkortning: $\frac{n\cdot a}{n \cdot b} = \frac{a}{b}$

, hvor $\frac{a}{b}$ er en vilkårlig brøk, og n er et vilkårligt positivt, helt tal.

Visuelt bevis

Visuelt kan dette begrundes ved blot at se på følgende:

$\frac{2}{4} = \frac{4}{8} = \frac{8}{16}$

Algebraisk argument (omformuleret version)

Da der i princippet står det samme ved både forlængning og forkortning, så kan man nøjes med at bevise det ene.

Ved forkortning står der således: $\frac{n\cdot a}{n \cdot b} = \frac{a}{b}$ .

Reelt står der på venstre side, at vi opdeler en enhed i $\frac{1}{n \cdot b}$ lige store stykker, hvor der skal ${n \cdot b}$ af dem for at danne en enhed på 1.

Tager man n af $\frac{1}{n \cdot b}$ – skrevet som $\frac{n}{n \cdot b}$ , så skal der altså b af disse stykker til at danne enheden 1.

I argumentet i bogen står der omformuleret i pkt 3, at $\frac{a}{b}$ kan tolkes som en angivelse af et stykke der består af a stykker af $\frac{1}{b}$ .

Det er sammenligneligt med, at der skal b stykker af $\frac{n}{n \cdot b}$ .

Derfor er $\frac{n}{n \cdot b}$ således det samme som $\frac{1}{b}$ .

Så $\frac{n}{n \cdot b}$ = $\frac{1}{b}$ .

Dog skal der a stykker af $\frac{1}{b}$ jf. venstre side af forkortningens ligning, hvilket derfor giver os $\frac{a}{b}$ .

Ergo er $\frac{n\cdot a}{n \cdot b} = \frac{a}{b}$

Addition af brøker

Her bruger vi det, at vi kan forlænge brøker. Ved at forlænge den første brøk med d og den anden med b, så skaber vi en fællesnævner. Dermed kan vi blot lægge tællerne sammen og beholder fællesnævneren.

$\frac{a}{b} + \frac{c}{d} = \frac{a \cdot d}{b \cdot d} + \frac{c \cdot b}{d \cdot b} = \frac{a \cdot d + b \cdot c}{b \cdot d}$

Subtraktion af brøker

$\frac{a}{b} - \frac{c}{d} = \frac{a \cdot d}{b \cdot d} - \frac{c \cdot b}{d \cdot b} = \frac{a \cdot d - b \cdot c}{b \cdot d}$

Tals delelighed

Det er en god idé at kende til tallenes delelighed, når man forkorter og forlænger brøker. Nedenunder har jeg derfor skrevet en række regler, der gør sig gældende nedenfor. De bygger på 3 sætninger for tallendes delelighed (delelighedssætning 1-3). Dem vil jeg ikke komme ind på her, men det gør vi muligvis senere.

Man siger, at et tal (divisor/faktor) går op (ved division) i et andet tal (dividenden), når der ikke er en rest. Tallet 12 har fx 1, 2, 3, 4, 6 og 12 (samt -12, -6, -4, -3, -2 og -1, men det er ofte underforstået at man kun medtager positive divisorer), som divisorer.

2 går op i et tal, når – og kun når – tallet ender på 0, 2, 4, 6 eller 8.
3 går op i et tal, når – og kun når – 3 går op i tallets tværsum.
4 går op i et tal, når – og kun når – 4 går op i det tal, der dannes af det oprindelige tals to sidste cifre.
5 går op i et tal, når – og kun når – tallet ender på 0 eller 5.
6 går op i et naturligt tal, når – og kun når – både 2 som 3 går op i tallet.
8 går op i et tal, når – og kun når – 8 går op i det tal, der dannes af det oprindelige tals tre sidste cifre.
9 går op i et tal, når – og kun når – 9 går op i tallets tværsum.
10 går op i et tal, når – og kun når – tallet ender på 0.
12 går op i et tal, når – og kun når – både 3 og 4 går op i tallet.
13 går op i et tal, når man kan tage tallet uden det sidste ciffer og derfra trække det ni-dobbelte af sidste ciffer. (Eksempel: 858 er deleligt med 13 fordi 85-9×8 = 13 er deleligt med 13)
14 går op i et tal, når – og kun når – både 2 og 7 går op i tallet.
15 går op i et tal, når – og kun når – både 3 og 5 går op i tallet.

Man kan finde et tals divisorer i Geogebra ved at anvende følgende funktioner:

Divisorliste [ ]

Brøker med Geogebra

Øvelserne 1 – 4 – opsamling.

Øvelse 1 – Udregn opgaverne. (se evt. videoerne under hjælp)

Øvelse 2 – Formuler selv et tilsvarende antal opgaver for samme område og med samme sværhedsgrad.

Øvelse 3 – Omskriv mellem brøker, decimaltal og procent. Formuler opgaver

Øvelse 4 – Procentopgaver fra FP9.

Brug evt. opgavegeneratoren på iundervisning.dk for brøkopgaver.

FFM og brøkbegreber

Hvad kan vi læse ud af læseplanen og målene? Hvilken type undervisning lægges der op til? Skriv en liste over de faglige begreber, I havde brug for, for at kunne løse og skrive opgaverne. Fx fællesnævner …

Skriv jeres opdagelser/bemærkninger ind på nedenstående padlet, som også kan findes på https://padlet.com/tgch/3rc7ttls5gn2.

Oplæg om brøker

Noter til øvelserne 9-12

Øvelse 9

$\frac{10}{12}$
$\frac{4}{5}$ – $\frac{5}{7}$ = $\frac{3}{35}$
a<2
Ved at gange den anden brøk (2) med den første brøks (1) nævner, så finder man, hvor stor tælleren ved den første brøk (1) maksimalt må være. Hvis værdien af den anden (2) brøk multipliceret med den første brøks (1) nævner giver et mindre tal end tælleren hos den første brøk (1), så er den første brøk (1) størst.
Det kan vises ved at sætte tal ind i stedet for a,b,c og d, men det kan også vises algebraisk. Husk at man kan forlænge eller forkorte med samme tal i både tæller og nævner – uden at brøken ændres. Det udnytter vi herunder: $\frac{a}{b} \leq \frac{c}{d} \Leftrightarrow$

$\frac{a \cdot d}{b \cdot d} \leq \frac{c \cdot b}{d \cdot b} \Leftrightarrow$ (forlænger) $\frac{a \cdot d}{b \cdot d} \cdot db\leq \frac{c \cdot b}{d \cdot b} \cdot db \Leftrightarrow$ $da\leq bc$
Det kan vises ved at sætte tal ind i stedet for a,b,c og d, men det kan også vises algebraisk. $\frac{a}{b} \leq \frac{a + c}{b + d} \Leftrightarrow$ $a \leq \frac{a + c}{b + d} \cdot b \Leftrightarrow$ $a \leq \frac{1}{b + d} \cdot (a + c) \cdot b \Leftrightarrow$ $a \cdot (b + d) \leq (a + c) \cdot b \Leftrightarrow$ $ab + ad \leq ba + bc \Leftrightarrow$ $ab + ad \leq ab + bc \Leftrightarrow$ $ab + ad - ab \leq ab + bc - ab \Leftrightarrow$ $ab \leq bc \Leftrightarrow$ $\frac{ad}{b} \leq \frac{bc}{b} \Leftrightarrow$ $\frac{ad}{b} \leq c \Leftrightarrow$ $\frac{a}{b} \cdot d \leq c \Leftrightarrow$ $\frac{a}{b} \leq \frac{c}{d}$
Det sidste var givet at være sandt, så derfor er også det ensbetydende udsagn $\frac{a}{b} \leq \frac{a + c}{b + d} \Leftrightarrow$ sandt.
Tilsvarende bevises $\frac{a + c}{b + d} \leq \frac{c}{d}$
Brug fx formlen fra øvelse 9, pkt. 6 til at finde en brøk mellem 1/7 og 1/8.

Øvelse 10

Øvelsen kunne også løses i CAS.

$\frac{7}{4}$
$\frac{13}{6}$
$\frac{1}{6}$
$\frac{17}{12}$
$\frac{5}{6}$
$\frac{38}{45}$
$\frac{26}{203}$

Øvelse 11

Forklaringsøvelse.

Hvilken repræsentation af stykket $\frac{2}{5} + \frac{1}{3}$ vil du foretrække? Brug nedenstående til at forklare ud fra.

Pizza
Rektangel
Lakridsstang

Den kan evt. diskuteres ud fra ggbm.at/C788kuD9.

Øvelse 12

Addition af brøker

$\frac{a}{b} + \frac{c}{d} = \frac{a \cdot d}{b \cdot d} + \frac{c \cdot b}{d \cdot b} = \frac{a \cdot d + b \cdot c}{b \cdot d}$

Subtraktion af brøker

$\frac{a}{b} - \frac{c}{d} = \frac{a \cdot d}{b \cdot d} - \frac{c \cdot b}{d \cdot b} = \frac{a \cdot d - b \cdot c}{b \cdot d}$

Hjælp

Her kan du finde nogle forklaringer på, hvordan man kan arbejde med brøker. Det skal ikke så selv, men blot ses, som en måde at gøre det på. Måske kan det hjælpe jer, hvis I sidder lidt fast.

www.youtube.com/user/iundervisningdk

Gode links

www.random.org/playing-cards

www.random.org/#numbers

Matematik

Matematik for lærerstuderende

M1-1E17NET – Program – 2017 – Uge 41– Dag 2

Kapitel 5 – De positive rationale tal

Brøker

Sætning 1 – At forkorte og forlænge brøker

Visuelt bevis

Algebraisk argument (omformuleret version)

Addition af brøker

Subtraktion af brøker

Tals delelighed

Brøker med Geogebra

Forkortning/Forlængning – Visualisering af brøker

Addition af brøker

Subtraktion af brøker

Division af brøker

Multiplikation af brøker

Øvelserne 1 – 4 – opsamling.

FFM og brøkbegreber

Oplæg om brøker

Noter til øvelserne 9-12

Øvelse 9

Øvelse 10

Øvelse 11

Øvelse 12

Hjælp

Gode links

Litteratur