Hermed følger programmet for uge 47. Vi arbejder hovedsageligt med Kapitel 9 i denne uge.
FORBEREDELSE
- Se modulplan.
UNDERVISNING
Primtal
Definition af primtal
Et primtal er et naturligt tal, som ikke kan skrives, som et produkt af to mindre naturlige tal.
Primtal er beskrevet af Euklid allerede 300 f.v.t. i sine bøger Elementerne. Han beskrev, at mængden af primtal er uendelig, men han angav ikke, hvordan man kunne finde frem til primtal. Det gjorde Eratosthenes fra Kyrene (276-194 f.v.t.) opfandt sin berømte si – kaldet Eratosthenes’ si.
Hans si kan beskrives vha. følgende definition:
Eratosthenes’ si
Hvis man vil finde alle primtal op til og med n2, skriver man alle tal op fra 2 til n2. For hvert primtal p mindre end eller lig med n slettes alle multipla af tallet (på nær p selv). Resten består af alle primtallene op til n2.
Forklaringen på side 169 i bogen viser, hvordan man fjerner alle sammensatte tal op til 16, nemlig 2,3,5,7,11 og 13.
Hvis vi har et sammensat tal a ⋅ b, som er mindre end eller lig med 16, så må enten a eller b være mindre end eller lig med 4.
Begge kan ikke være mere end 4, da det ville give mere end 16. Hvis den ene er 4, så må det andet altså være mindre end eller lig med 4. Det betyder, at ethvert tal op til og med 16 har 2, 3 eller 4 som faktor. Da 4 ikke er et primtal, men kan beskrives som 2 ⋅ 2, så kan vi nøjes med at beskrive alle tal op til og med 16 vha. primtallene 2 og 3.
Man kalder denne primfaktoropløsning.
Eksempel
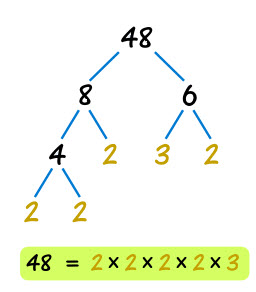 Ethvert tal større end 1 er enten et primtal eller et sammensat tal. Et sammensat tal kan dog altid beskrives, som to tal multipliceret med hinanden. Fx kan tallet 6 beskrives som 2 ⋅ 3, og tallet 8 kan beskrives som 2 ⋅ 4.
Ethvert tal større end 1 er enten et primtal eller et sammensat tal. Et sammensat tal kan dog altid beskrives, som to tal multipliceret med hinanden. Fx kan tallet 6 beskrives som 2 ⋅ 3, og tallet 8 kan beskrives som 2 ⋅ 4.
Ved primfaktorisering/primfaktoropløsning bliver man dog ved, indtil man ikke har flere sammensatte tal i regneudtrykket. Det betyder, at 8 kan beskrives, som 2 ⋅ 4. Men da 4 også er et sammensat tal, som kan beskrives ved 2 ⋅ 2, så kan 8 beskrives som 2 ⋅ 2 ⋅ 2. Dette kan også skrives som 23.
Man kan anvende et tælletræ til at forenkle processen, som vist her til venstre.
Primfaktorisering/primfaktoropløsning
Herunder en dansk udgave af en video fra khanacademy.com.
Noter til øvelserne 1-14
Øvelse 1
Definition 1
Hvis d og D er naturlige tal, så siger vi, at d går op i D, hvis der findes et naturligt tal q, således at D = d ⋅ q.
Dermed kan vi sige, at
- 91 = 7 ⋅ 13, så 7 går op i 91; kvotienten er 13.
D = d ⋅ q - 143 = 13 ⋅ 11, så 13 går op i 143; kvotienten er 11.
D = d ⋅ q - – Alternativ version –
Øvelse 2
Sætning 1
Hvis d går op i både D1 og D2, så går d op i D1 + D2.
Sætning 2
Hvis d går op i både D1 og D2, så går d op i D1 – D2.
Direkte bevis
D1 + D2.
Først kigger vi på d går op i D1 og D2. Dermed må det jf. definition 1 betyde D1 = d ⋅ q1 og D2 = d ⋅ q2, hvor q1 og q2 er naturlige tal.
Vi lægger sammen og får D1 + D2 = d ⋅ q1 + d ⋅ q2. = d ⋅ (q1 + q2)
Men da (q1 + q2) er et naturligt tal (det er jo 2 naturlige tal lagt sammen), så kan man kalde det q. Så dermed kan vi sige, at der nu står D1 + D2 = d ⋅ q, hvilket jf. definition 1 betyder, at d går op i D1 + D2. Hvilket skulle bevises.
D1 – D2 for D1 > D2
Først kigger vi på d går op i D1 og D2. Dermed må det jf. definition 1 betyde D1 = d ⋅ q1 og D2 = d ⋅ q2, hvor q1 og q2 er naturlige tal.
Dermed trækker vi dem fra hinanden og får D1 – D2 = d ⋅ q1 – d ⋅ q2. = d ⋅ (q1 – q2)
Men da (q1 – q2) er et naturligt tal (det er jo 2 naturlige tal trukket fra hinanden), så kan man kalde det q. Så dermed kan vi sige, at der nu står D1 – D2 = d ⋅ q, hvilket jf. definition 1 betyder, at d går op i D1 – D2. Hvilket skulle bevises.
Øvelse 3
- Find alle primtal op til 100 vha. Erastothenes’ si:
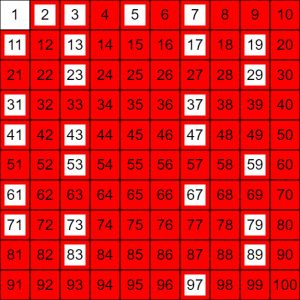
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61,
67, 71, 73, 79, 83, 89 og 97. - Søgning: sieve eratosthenes interactive
- Gode links til Eratosthenes Si
- Primtalstvillinger
Par (3,5) Par (5,7) Par (11,13) Par (17,19) Par (29,31) Par (41,43) Par (59,61) Par (71,73)
Øvelse 4
Det ene af tallene (p, p + 1) er lige. Det eneste lige primtal der findes er 2. Derfor kan der kun
findes ét sæt primtalsnaboer, nemlig (2,3).
Når p er ulige, vil der blandt tallene (p, p + 2, p + 4) altid være ét, der ligger i 3-tabellen, fordi det er
åbenlyst, at et af de tre på hinanden følgende tal (p, p + 1, p + 2) må ramme 3-tabellen, og hvis det
er p + 1, så vil p + 4 også gøre det. Da det eneste primtal i tretabellen er selve 3, kan der kun være
det ene sæt primtalstrillinger (3, 5, 7).
f(n) = n2 – n + 41 ser ud til at give lutter primtal. Dog får man et sammensat tal, når man indsætter 41.
Prøv evt at bruge regnearket til at lave værdierne.
Download regneark: primtal-op-til-3000
Øvelse 5
–
Euklids algoritme
Euklids algoritme kan bruges til at finde den største fælles divisor til to tal. Altså det største tal, som går op i to forskellige naturlige tal. Jeg viser det med to andre tal end dem, som er givet i bogen. Han benyttede de to sætninger nedenfor. De er også brugt i øvelse 2.
Sætning 1
Hvis d går op i både D1 og D2, så går d op i D1 + D2.
Sætning 2
Hvis d går op i både D1 og D2, så går d op i D1 – D2.
Eksempel 1 – Find Største Fælles Divisor
Lad os sige, at vi tager tallene 112 og 36. Så finder man den største fælles divisor ved at trække det mindste tal fra det største tal. 112-36 = 76. Igen 76-36 = 40. Igen 40-36 = 4. Man skal dog blive ved at trække tallene fra hinanden indtil begge tal bliver lige store. Da man ikke kan trække 36 fra 4 uden at få et negativt tal og dermed ikke et naturligt tal, så bytter man blot om på tallene, så man trækker det mindste fra det største. Man fortsætter 36-4 = 32, 32-4 … 8-4 = 4. 4 er dermed den største fælles divisor.
Eksempel 2 – Find Største Fælles Divisor
Den største fælles divisor til 446 og 248 er 446-248 = 198. 248-198 = 50, 198-50 = 148, 148-50 = 98, 98-50 = 48, 50-48 = 2. Dermed er den største fælles divisor altså 2.
Eksempel 2 – Find Største Fælles Divisor
Den største fælles divisor til 850 og 250 er 850-250 = 600, 600-250 = 350, 350 – 250 = 100, 250 – 100 = 150, 150-100 = 50, 100-50 = 50. Den største fælles divisor er dermed 50.
Det er dog en temmelig vanskelig og omstændelig måde, hvis man har store tal. Derfor kan man benytte metoden division med rest.
Værktøj
Du kan også bruge følgende regneark til at finde Største Fælles Divisor og Mindste Fælles Multiplum.
Øvelse 6 – Division med rest
| Rest | ||
| 330 | 77 | 22 |
| 77 | 22 | 11 |
| 22 | 11 | 0 |
Den største fælles divisor er derfor 11.
Prøv denne metode på tallene: 279 og 117 (Se svaret ved at markere teksten)
| Rest | ||
| 279 | 117 | 45 |
| 117 | 45 | 27 |
| 45 | 27 | 18 |
| 27 | 18 | 9 |
| 18 | 9 | 0 |
Den største fælles divisor er derfor 9.
——————————————————————————-
Vi springer denne del over i denne omgang. Vi kigger på det i modul 3. Se det derfor ikke som endelige svar eller forklaringer. Jeg går derfor ikke i dybden med det denne gang.
Sætning 3 – Følgesætning til Euklids algoritme
Følgesætning til Euklids algoritme kan bruges til at finde løsninger til såkaldte diophantiske ligninger, som er ligninger, hvor alle indgående tal er hele.
Følgesætningen kan beskrives som
sfd(D,d) = x ⋅ D + y ⋅ d, hvor x og y er hele tal (Talmængde Z).
Hvis man vil finde ud af, om der findes heltallige løsninger a og b til en ligning, så kan man bruge Euklids følgesætning.
Øvelse 7
Hvis man derfor har to tal 25 og 17, som har fælles divisor 1, så kan man sætte dem ind i Euklids følgesætning, så man får x ⋅ 25 + y ⋅ 17 = 1. Eller skrevet som 25 ⋅ x + 17 ⋅ y = 1. Tallet 1 kan altså skrives som 25 ⋅ x + 17 ⋅ y, hvor x og y er hele tal. Nu er det blot at finde løsningen. Den er 25 · (-2) + 17 · 3 = 1.
Undersøgelse 1
Afgør, om der findes løsninger til ligningerne:
- 17x + 25y = 1
Sfd(25,17) = 1
Løsninger JA. - 15x + 25y = 6
Da sfd(25,15) = 5 findes der jf. følgesætningen løsninger til ligningen 15a + 25b = 5, men 15(x – a) + 25(y – b) = 1.
Løsninger NEJ. - 42x + 33y = 6
Da sfd (42,33) = 3 findes der løsninger til ligningen 42a + 33b = 3.
Dermed er x= 2a og y = 2b løsning til ligningen 42x + 33y = 6.
Løsninger JA. - 65x + 91y = 6
Da sfd (91,65) = 13 findes der jf følgesætningen løsninger til ligningen 65a + 91b = 13.
Men da - —
- —
- —
- —
Sætning 4
Hvis et primtal går op i et produkt, går det op i en af faktorerne.
Bevis
Hvis et primtal p går op i et produkt ab, må p gå op i mindst én af faktorerne a og b.
Hvis vi eksempelvis ser på, om primtallet 7 går op i 21, så ser vi, at 7 altså må gå op i enten 3 eller 7.
Det bevises indirekte ved at påvise, at såfremt p ikke går op i b, så må p gå op i a.
Vi siger altså, at p går op i ab, men ikke i b.
Hvis p ikke går op i b, så må sfn(p,b) være lig med 1, fordi p kun har faktorerne p og 1, da det jo er et primtal.
Bruger vi sætning 3, så ved vi, at der findes hele tal x og y, så x ⋅ p + y ⋅ b = 1.
Ganger vi igennem med a, så får vi, at x ⋅ p ⋅ a + y ⋅ b ⋅ a = 1 ⋅ a. Det kan også skrives som p ⋅ x ⋅ a + a ⋅ b ⋅ y = a.
Her kan vi se, at p faktisk går op i 1. og 2. led på venstre side, da p går op i p i første led og i ab i 2. led. Da venstre side er lig med højre side, så må p altså også gå op i a, hvilket skulle bevises.
Øvelse 8
—
Øvelse 9
- 18 = 2 ⋅ 32
- 750 = 2 ⋅ 3 ⋅ 53
- 143 =11 ⋅ 13
Øvelse 10
Man finder antallet af divisorer ved at se på, hvor mange potenser, det er muligt at bruge af det enkelte primtal.
Hvis et sammensat tal som 92 fx. skal beskrives vha. primtal (kaldet primfaktoropløsning), så kan det skrives som 92 = 2 · 2 · 23.
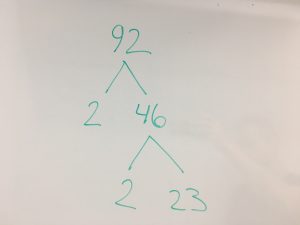
Dermed kan vi lave et tælletræ/procesdiagram, som starter med at have 3 mulige udfald til divisorer, nemlig 20, 21 og 22. I næste led i tælletræet er der 2 mulige udfald til divisorer, da det er 230 og 231.
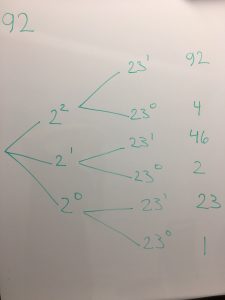
Ialt er der således 3 · 2 = 6 mulige divisorer. Det er 1, 2, 4, 23, 46 og 92. Dette er forklaret på side 180 i bogen. Vi bruger det i øvelse 10.
- 12 = 3 ⋅ 22 og 75 = 3 ⋅ 52
Derfor er de begge på formen p ⋅ q2 og har divisorerne p, q , p ⋅ q og p ⋅ q2. - 210 = 2 ⋅ 3 ⋅ 5 ⋅ 7
Divisorerne er derfor- 20 ⋅ 30 ⋅ 50 ⋅ 70 = 1,
- 21 ⋅ 30 ⋅ 50 ⋅ 70 = 2
- 20 ⋅ 31 ⋅ 50 ⋅ 70 = 3,
- 20 ⋅ 30 ⋅ 51 ⋅ 70 = 5,
- 21 ⋅ 31 ⋅ 50 ⋅ 70 = 6,
- 20 ⋅ 30 ⋅ 50 ⋅ 71 = 7,
- 21 ⋅ 30 ⋅ 51 ⋅ 70 = 10,
- 21 ⋅ 30 ⋅ 50 ⋅ 71 = 14,
- 20 ⋅ 31 ⋅ 51 ⋅ 70 = 15,
- 20 ⋅ 31 ⋅ 50 ⋅ 71 = 21,
- 21 ⋅ 31 ⋅ 51 ⋅ 70 = 30,
- 20 ⋅ 30 ⋅ 51 ⋅ 71 = 35,
- 21 ⋅ 31 ⋅ 50 ⋅ 71 = 42,
- 21 ⋅ 30 ⋅ 51 ⋅ 71 = 70,
- 20 ⋅ 31 ⋅ 51 ⋅ 71 = 105,
- 21 ⋅ 31 ⋅ 51 ⋅ 71 = 210,
- Hvilke(t) tal under 100 har fleste divisorer?
60 = 2 · 2 · 3 · 5 , 72 = 2 · 2 · 2 · 3 · 3 , 84 = 2 · 2 · 3 · 7, 90 = 2 · 3 · 3 · 5 og 96 = 2 · 2 · 2 · 2 · 2 · 3 har alle 12 divisorer. - Tal med netop 2 divisorer er primtal.
- Hvad kan du fx sige om tal med præcis tre divisorer?
- –
Øvelse 11
- Så findes der 3 · 4 divisorer. Altså 12.
- Hvis p · q · r er 3 forskellige primtal, så er der 8 divisorer
- p0 · q0 · r0,
- p1 · q0 · r0,
- p0 · q1 · r0,
- p1 · q1 · r0,
- p0 · q0 · r1,
- p1 · q0 · r1,
- p0 · q1 · r1,
- p1 · q1 · r1,
- Hvis p er et primtal, så har pn netop (n+1) divisorer.
Divisorerne er 1, p1, p2, p3, p4, pn-1,pn. Altså n+1 divisorer. - –
- Fra punkt 4 ved vi at der til ethvert tal findes px · qy · … · rz, har (x+1) · (y + 1) · … · ( r + 1) divisorer.
Det betyder, at alle faktorerne på nær én kun kan være 1 og den sidste må være 11. Det må være et primtal, som er opløftet i 10’ne potens. 210 er 512. 310 er 59049, hvilket er mere end 2000.
Tallet under 2000, der har 11 divisorer er derfor 512.
Få evt. hjælp fra dette link.
en.wikipedia.org/wiki/Table_of_divisors
Øvelse 12
- sfd(72,25)
Da 72 = 23 · 32 og 25 = 52 er sfd(72,25) = 1, idet de ikke har et fælles primtal, som således kan “gå op”.
I mfm(72,25) skal alle primfaktorerne derfor indgå med maksimal vægt. Dvs. 23 · 32 · 52 = 1800. - Fx 2 · 33 · 52 og 33 · 52.
Sfd af de to tal er 33 · 52 og mfm er 2 · 33 · 52. - Hvis man skal finde eksempler, hvor forskellen på sfd og mfm er lille, så skal de to tal indeholde de samme primfaktorer med fx kun et 2-tal som afvigelse.
- At der for vilkårlige naturlige (positive hele tal) tal a og b gælder mfm(a,b) · sfd(a,b) = a · b kan holdes på mindre symbolkrævende plan, hvis man konstaterer, at a · b indeholder alle de forekommende primfaktorer i a og b, men det gør mfm(a,b) også, idet dog de primtal, der er fælles for a og b, ikke kommer med to gange, men de kommer med i sfd(a,b), hvor de netop kommer med i den lavere potens, der blev udeladt i mfm(a, b). Derfor kommer alle primfaktorer i a og b med i den rette potens, når man multiplicerer mfm(a,b) og sfd(a,b).
Et eksempel
mfm(6,4) · sfd(6,4) = 6 · 4
( 22 · 3) · 2 = (2 · 3) · (2 · 2)
23 · 3 = 23 · 3
24 = 24
Øvelse 13
Vis, at er irrational.
Her laver jeg et indirekte bevis, som vist i bogen på side 183. Vi antager altså, at ikke er irrational, men rational. Det må betyde, at
kan skrives som en brøk
.
Vi vil kunne skrive
Det ville betyde, at
.
.
Men den eneste uforkortelig brøk, som er lig med 17 er .
Dermed er p2 = 17 og q2 = 1.
Men der er ikke et tal, som multipliceret med sig selv, giver 17, da 17 er et primtal.
Antagelsen om, at var altså forkert, og derfor er
irrational.
De eneste tal, som kan beskrives som rationale, er kvadrattallene.
Øvelse 14
Et indirekte bevis vil igen være at antage, at er rationalt tal, så får vi
.
Det betyder, at n = p2, da q altid må skulle være 1. Den eneste situation, hvor dette ikke giver anledning til en modstrid, er hvis n er et kvadrattal.
Altså er irrational på nær, når n er et kvadrattal.
Pernille Pind
Én forkert – Løsninger i regneark
LITTERATUR
