Hermed følger programmet for dag 1 i uge 39. Vi arbejder hovedsageligt med Kapitel 5 i denne uge.

DAG 1

FORBEREDELSE

Genlæs ‘Indledende brøkregning’ .

Læs ‘Videregående regning med brøker’ .

Lav øvelserne 13-18 .

UNDERVISNING

Brøker

Bogens fortolkning af brøker kan kort formuleres således:

En brøk er en ligelig opdeling af en enhed. Vi deler en enhed i b lige store dele. Fx kan vi dele 20 æg i 4 lige store dele, hvilket er 5 æg til hver fjerdedel.
Hver af disse dele kalder vi en b’endedel, hvilket skrives som $\frac{1}{b}$ .
a bliver da en angivelse af, hvor mange af de $\frac{1}{b}$ .’endedele, vi tager. Vi tager $a \cdot \frac{1}{b}$ , hvilket skrives som $\frac{a}{b}$ . Fx tager vi 3 af $\frac{1}{4}$ , hvor hver fjerdedel svarer til 5 æg. Det giver samlet 15 æg. Så $\frac{3}{4}$ af 20 æg er lig med 15 æg.

Sætning 1 – At forkorte og forlænge brøker

Brøker kan multipliceres med samme hele tal i tæller og nævner, uden at brøken derved ændrer størrelse. Dette kan udtrykkes symbolsk som:

Forlængning: $\frac{a}{b} = \frac{n\cdot a}{n \cdot b}$ Forkortning: $\frac{n\cdot a}{n \cdot b} = \frac{a}{b}$

, hvor $\frac{a}{b}$ er en vilkårlig brøk, og n er et vilkårligt positivt, helt tal.

Visuelt bevis

Visuelt kan dette begrundes ved blot at se på følgende:

$\frac{2}{4} = \frac{4}{8} = \frac{8}{16}$

Algebraisk argument (omformuleret version)

Da der i princippet står det samme ved både forlængning og forkortning, så kan man nøjes med at bevise det ene.

Ved forkortning står der således: $\frac{n\cdot a}{n \cdot b} = \frac{a}{b}$ .

Reelt står der på venstre side, at er der et vist antal af enheden $\frac{1}{n \cdot b}$ lige store stykker, hvor der skal ${n \cdot b}$ af dem for at danne en enhed på 1.

Tager man n af $\frac{1}{n \cdot b}$ – skrevet som $\frac{n}{n \cdot b}$ , så skal der altså b af disse stykker til at danne enheden 1.

I argumentet i bogen står der omformuleret i pkt 3, at $\frac{a}{b}$ kan tolkes som en angivelse af et stykke der består af a stykker af $\frac{1}{b}$ .

Det er sammenligneligt med, at der skal b stykker af $\frac{n}{n \cdot b}$ .

Derfor er $\frac{n}{n \cdot b}$ således det samme som $\frac{1}{b}$ .

Så $\frac{n}{n \cdot b}$ = $\frac{1}{b}$ .

Dog skal der a stykker af $\frac{1}{b}$ jf. venstre side af forkortningens ligning, hvilket derfor giver os $\frac{a}{b}$ .

Ergo er $\frac{n\cdot a}{n \cdot b} = \frac{a}{b}$

Addition af brøker

Her bruger vi det, at vi kan forlænge brøker. Ved at forlænge den første brøk med d og den anden med b, så skaber vi en fællesnævner. Dermed kan vi blot lægge tællerne sammen og beholder fællesnævneren.

$\frac{a}{b} + \frac{c}{d} = \frac{a \cdot d}{b \cdot d} + \frac{c \cdot b}{d \cdot b} = \frac{a \cdot d + b \cdot c}{b \cdot d}$

Subtraktion af brøker

$\frac{a}{b} - \frac{c}{d} = \frac{a \cdot d}{b \cdot d} - \frac{c \cdot b}{d \cdot b} = \frac{a \cdot d - b \cdot c}{b \cdot d}$

Videregående regning med brøker

Multiplikation og division af brøker

Generelt kan man sige, at der netop ved disse to regnearter mangler hverdagserfaringer, hvor det giver mening at multiplicere brøker med hinanden. Det giver fx ikke mening at gange $\frac{1}{2}$ pizza med $\frac{1}{3}$ pizza. Vi finder dog opgaver, som kan give mening, i det brøkspil ‘Brøker i hverdagen’, som I prøvede sidste gang.

Multiplikation af brøker

Når man multiplicerer brøker med hinanden, så svarer det til at man finder en brøkdel af noget, som allerede er en (brøk)del. Fx en $\frac{1}{2}$ af en $\frac{1}{3}$ sodavand.

Vi deler jf definitionen på en brøk således den anden brøk i b’endedele først. De dele er nu $\frac{1}{b}$ ‘endedele. Af dem tager vi så a stykker. I eksemplet med sodavanden ovenfor er det derfor at forstå sådan, at $\frac{1}{3}$ sodavand deles i 2 dele. Det bliver derfor delt i 2 gange så mange stykker. Det er altså nu 6-dele og af dem tager vi 1. Vi har taget $\frac{1}{6}$ .

Division af brøker

Her skal I tænke måledivision. I skal således finde ud af, hvor mange gange en given brøk kan “være/gå op i en brøk”. Fx hvor mange kvarte liter fløde, der går på tre kvarte liter fløde. Altså $\frac{3}{4}$ : $\frac{1}{4}$ .

Man dividerer $\frac{a}{b}:\frac{c}{d}$ ved at gange $\frac{a}{b}$ med den omvendte brøk af $\frac{c}{d}$ . Dermed får man, at $\frac{a}{b}:\frac{c}{d}$ = $\frac{a}{b} \cdot \frac{d}{c}$ .

Det kan ses herunder:

$\frac{a}{b}:\frac{c}{d}$

= $\frac{a\cdot d}{b\cdot d}:\frac{c\cdot b}{d\cdot b}$ (Vi forlænger begge brøker)

= $\frac{a\cdot d}{b\cdot d}:\frac{b\cdot c}{b\cdot d}$ (Stiller det korrekt)

Da vi nu har samme nævner (kaldet fællesnævner), så står der egenligt blot.

= ad : bc

= $\frac{ad}{bc}$

Hvilket er

= $\frac{a \cdot d}{b\cdot c}$

og altså

= $\frac{a}{b} \cdot \frac{d}{c}$

Ergo er

$\frac{a}{b}:\frac{c}{d}$ = $\frac{a}{b} \cdot \frac{d}{c}$

Noter til øvelserne 13-18

Øvelse 13

Jeg ville forsøge at bruge billeder/situationer, som eleven kender fra hverdagen. Det kunne være sodavand, kager, chokolade. Når man multiplicerer brøker med hinanden, så svarer det til at man finder en brøkdel af noget, som allerede er en (brøk)del. Fx en $\frac{1}{3}$ af en $\frac{1}{2}$ sodavand. Jeg ville bede eleven tegne det og spørge til, hvad fællesnævneren er blevet til.

$\frac{1}{3}$ af det halve af en kage/cirkel. Det er $\frac{1}{6}$ .

Det kan være en god idé at forlænge brøkerne, så de får samme fællesnævner. Dermed kan det blive tydeligere for eleven, hvad der reelt regnes på, når man regner med division af brøker. Se herunder:

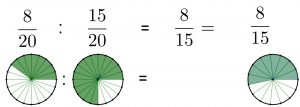
Brøkerne i regnestykket $\frac{2}{5} : \frac{3}{4}$ forlænges til $\frac{8}{20} : \frac{15}{20}$ . De $\frac{15}{20}$ går således kun $\frac{8}{20}$ op i $\frac{8}{20}$ .

Øvelse 14

$\frac{9}{28}$
$\frac{4}{9}$
1
4
$\frac{3 \cdot n}{4}$
5

Øvelse 15

Personlig argumentation: Jeg ville bruge repræsentationerne fra sidste gang (rektangel, pizza, lakridsstang) samt links til ‘brøker i Geogebra’. Det handler om måledivision. Altså, hvor mange gange noget “går op i”.

Øvelse 16

$\frac{9}{8}$ eller $1 \frac{1}{8}$
$\frac{7}{24}$

Øvelse 17

Opgaven kan forklares på 2 måder (sikkert flere).

25 liter delt med $\frac{3}{4}$ findes ved at gange med den omvendte, hvilket er $\frac{100}{3}$ . Det er 33 flasker og $\frac{1}{3}$ til rest, hvilket er nok til en smagsprøve, da $\frac{1}{3}$ af en flaske på $\frac{3}{4}$ liter er $\frac{1}{4}$ liter.

Det tages først $\frac{1}{4}$ liter fra til en smagsprøve af de 25. Tilbage er der $24 \frac{3}{4}$ . Flaskerne kan indeholder $\frac{3}{4}$ liter. Jeg ville lave vinballonen om til uægte brøk først og derefter dividere den med de $\frac{3}{4}$ liter. Regnestykket er således $\frac{99}{4} : \frac{4}{3} = 33$ .

Øvelse 18

Tre tekstopgaver med multiplikation af brøker og tre med division af brøker.

Multiplikation

Hvad er $\frac{3}{4}$ af en kvart melon?
Troels vil gerne lave en kage. Han har 3/4 kg sukker, men han skal kun bruge $\frac{1}{2}$ af det. Hvor meget sukker skal han bruge?
Louies far vil lave Pizza. Han skal bruge $\frac{2}{5}$ af en $\frac{1}{2}$ pakke smør på 250g. Hvor meget smør skal han bruge?

Division

Mads’ mor vil lave jordbærmarmelade. Hun laver 9 $\frac{1}{2}$ liter. Hvor mange krukker skal hun bruge, hvis der i hver krukke kan være $\frac{1}{4}$ liter?
–
–

Næste gang

Genlæs ‘Indledende brøkregning’ .
Læs ‘Videregående regning med brøker’ .
Lav øvelserne 19-25 .

Matematik

Matematik for lærerstuderende

M1-1E17 – Program – 2017 – Uge 39 – Dag 1